(part 1, part 2, part 3, part 4)

Last time we determined that beta neutral spreads are the perfect instrument to use in our speculative portfolio.  Now we need to decide which spreads.  Sadly, that’s as open ended a question as “Which stock should I buy?”.  What I’m going to share with you here is a technique I’ve developed that seems to give good returns on relatively low risk.

Years ago, before I decided that conventional investing was a bad idea, I spent a lot of time looking into dividend stocks.  There are of course portions of the financial internet that are flat out in love with dividend stocks.  Usually they throw in a good dose of Warren Buffett fanaticism for good measure.  I’ve come to believe that the Buffett stuff is 90% bullshit, but that’s a story for a different day.  The main point is that I was looking at a lot of high-dividend stocks, and if I was going to buy them as investments I wanted to get a good deal.  So I asked a very simple question: How do I know when a dividend stock is cheap?

One potential answer lies in the theory for pricing cash flows.  If we model a dividend stock as simply providing a guaranteed series of dividend payments, then the stock functions in effect turns into the interest-only (IO in bond trader lingo) portion of a AAA bond.  And like any bond, its price should move opposite of yield.  This simplistic model suggests that dividend stocks should behave in an odd fashion – when the market is in the dumps and drives T-bond yields down (and bond prices up), dividend stocks should move with them.  Yield down, price up.

Now, if you look at the way the market actually behaves, you’ll see this phenomenon happening on the long term but not on the short term.  We’ve now had almost 4 years of persistently low bond rates since the 2008 crash.  Initially, nearly every dividend stock tanked along with the rest of the market, which is contrary to the theory above.  But during the recovery they’ve outperformed, with most exceeding their 2007/8 highs as low bond yields cause yield-seeking behavior and drive money into the safer segments of the stock market.

Any time you see a relationship that holds in the long term, but not in the short term, you should start to get the feeling that there’s money to be made betting against the short term.  Which is exactly where I’m going, but we need to make a few more stops along the way.  My model of treating a dividend stock as a long-term IO bond has some flaws.  First off, it assumes a constant dividend rate into the future when in reality successful companies can increase their dividend over time.  Similarly, it assumes a zero chance of the company failing which is clearly unrealistic.  These differences between theory and reality making pricing dividend stocks via fundamentals much harder than I’ve implied – in fact so hard that maybe no one does it consistently well.  I don’t claim any particular expertise.  In fact, I’m rather lazy so I’d like to avoid the problem at all and let the market do as much work as possible for me.  Which raises a second question: What can the market tell me about correct pricing for a dividend stock?

One thing we do know about certain stocks with long-standing dividends is that they’re boring.  Because most of the earning are returned to the shareholders, growth is limited.  This is both good and bad.  It reduces the likelihood of the company embarking on some new and profitable enterprise, but it also prevents them from spending money on some idiotic turkey of an idea.  Large dividends mute both the upside and downside potential, and thus the historic behavior of a dividend stock is probably a pretty good indication of where its going.  This leads us to a another simplistic model for dividend stock pricing:

The correct price of a dividend stock is its average price over some period of time.  The distance between the current price and the average price, measured in standard deviations, tells us how mispriced it currently is.

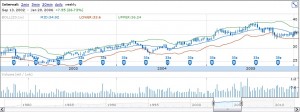
Now once again this is a painfully simplistic model that misses all sorts of real issues.  But it’s a starting point in that it uses the market, via averaging and standard deviation calculations, to get a handle on all the problems with our first bond-based pricing model.  In order to understand how this new model works it’s helpful to look at the price chart of a dividend stock annotated with a moving average of price and standard deviation bands for price.  This sort of chart is frequently referred to as Bollinger bands, and you don’t need a complicated charting package to see them.  Google finance charts includes a perfectly usable version.  As an example I’ve charted 3 years of weekly bars of NWN stock, which is a long-standing dividend paying natural gas producer. The moving average (middle) line has a 20 week period and the Bollinger bands are set two standard deviations out:

You can see that over a 3 year period NWN saw only limited price change in the $25-40 range.  These are actually three of the more exciting years NWN has had, which is why I chose them for the example plot since our eventual strategy will be based on a lack of long term volatility, and if it still works in the face of some long term moves then it will likely work consistently.

Now, there’s something wrong with this chart, but if you don’t know what to look for you’d likely never spot it.  It turns out, if the pricing of an instrument is efficiently generated by a random walk, that it will spend about 2.2% of its time more than 2 standard deviations above the average price and the same amount of time 2 standard deviations below.  That means in the three years covered by this chart, we would expect about 7 of the 156 weekly closing prices to be outside the Bollinger bands.  A whopping seventeen of them are.  In other words, the distribution of prices here does not look the way we would expect.  Instead of having the typical normal distribution that a random walk and the central limit theorem would imply, it must be fatter in the “shoulders” of the curve slightly past 2SD and therefore thinner in both the tails and middle.  It turns out this pattern repeats for a large family of dividend stocks.  Hmm…

Thin tails correspond directly to part of our theory about dividend stocks – namely that they ‘re boring and don’t exhibit massive long term price moves.  But the relatively thin middle is odd – that means price has a tendency to blow from one extreme to the other, lingering in the middle less than you would expect.  In other words what we’re seeing here is a sort of mean reversion behavior with overshoot – prices go to one extreme, and then more often than not move back to the middle, overshoot, and go to the other side where the pattern repeats.  The stock is boring at extreme prices, but surprisingly mobile in the middle.  You can see this phenomenon in the chart above – the average bar that crosses the middle line is bigger than the average bar that doesn’t.

At this point, we could simply stop thinking and lay out our trading strategy: buy dividend stocks when they close below the lower 2 SD band.  Sell to close when they revert to the mean.  Similarly, sell short when they close above the 2 SD band and buy to close at the mean.  This I would argue is a winning strategy, but it’s not best from a risk perspective and it lacks a good solid explanation as to why it works.  For that explanation we need to talk about program trading.

Program trading is, in essence, the man behind the curtain in the stock market.  Not that there’s anything particularly sinister about it, but program trading is both the dominant force in equities and almost completely ignored or misunderstood by the public and retail traders.  Slightly over 50% of stock trades have a program trade as one side or the other and program trades make up 30-40% of daily share volume on the major exchanges.  This number has been growing.

A program trade is defined as any time one party in the market trades simultaneously in a large basket of stocks.  Program trades are so named because, if you want to trade a bunch of stocks at once, you need a computer programmed to do it.  By itself the term doesn’t imply why someone is trading so many stocks at once, just that they’re doing it.  That said, most program trades follow a certain internal logic which can best be explained in the context of index futures and index arbitrage.  An index future is simply a vehicle for trading the value of some stock index in a clean way.  For example, the ES future represents the S&P500 index.  Now, it should be obvious that there’s an arbitrage relationship between the index future and the stocks comprising the index.  If the futures go up the stocks should go up and vice versa.  Index arbitragers police this relationship.  If someone comes along and buys a bunch of ES, the arbitrageurs sell them the ES and buy the 500 components of the S&P500 to get back to a conceptually flat position.  As you’ve probably guessed, buying 500 stocks at once is a program trade.

There are a lot of complex variants on program trading, but they all follow the same basic logic.  You have some basket of stocks, and some opinion about what they “ought” to be priced at.  Perhaps you’re trading oil company stocks vs. oil prices.  Perhaps you’re trading healthcare stocks vs. a healthcare ETF.  Perhaps you’re trading troubled companies vs. an index that tracks their likelihood of bond default.  But the key point is you’ve got a basket of stocks and something that you think tells you what the price should be.  When the basket is overpriced, you sell.  When it’s underpriced, you buy.

Now, you may be wondering what this has to do with our dividend stocks.  The answer is this: I believe program trading distorts the price of dividend stocks.  The reason is that most non-program trading people active in dividend stocks are following very conservative Benjamin Graham style investment strategies.  These strategies have very widely seperated buy and sell points defined by something Graham called the “margin of safety”.  In essence, you buy only when things are very cheap, sell only when very expensive, and sit tight the rest of the time.  What this means is that if you push the price of a dividend stock low enough via program trading, the market will suddenly firm up as Graham style investors achieve the margin of safety they need to invest.  Similarly, if you push prices high enough you’ll exhaust their margins and cause them to sell, putting in a ceiling.

This, I think, explains the “slow moving at extreme prices, fast moving at average prices” phenomenon we saw in the charts.  And it’s definitely a tradeable inefficiency.  Here are the trading rules I’m currently using:

• Build a watch list starting with the dividend championstocks
  • Eliminate all stocks with dividends greater than earnings or projected earnings
  • Eliminate all stocks with market caps less than $1B or known to have very thin markets
  • Eliminate all stocks that exhibit strong trending behavior
  • Eliminate all stocks with a beta greater than 0.6 (this gives us the most boring ones, plus has some portfolio allocation advantages)
  • Re-build the watch list each year.
• The watch list for 2012: ABT, BMS, CLX, GPC, JNJ, NWN, PEP, PNY, PG, SYY, WGL
• Wait for one of these stocks to move more than 2 standard deviations from the 20-bar mean on weekly bars.  Then wait for it to move slightly towards the mean.  Then enter a beta-neutral spread betting the stock will return to the mean value.
• Exit this spread when the stock returns to the mean value.

And there you have it: the top secret method.  There’s still quite a few things we need to go over – portfolio allocation, risk management, and what if anything we want to do about bonds and commodities.  But this is the guts of the speculative alternative to investment.

The next installment will cover the last of the details, lay out a model portfolio, give you a spreadsheet to build your own, and report some initial performance results.

Continued in part 6.